SS-V:9004 導電性材料を持つ共振器
テスト番号VE05導電性材料で満たされた共振器のモーダル解析
定義
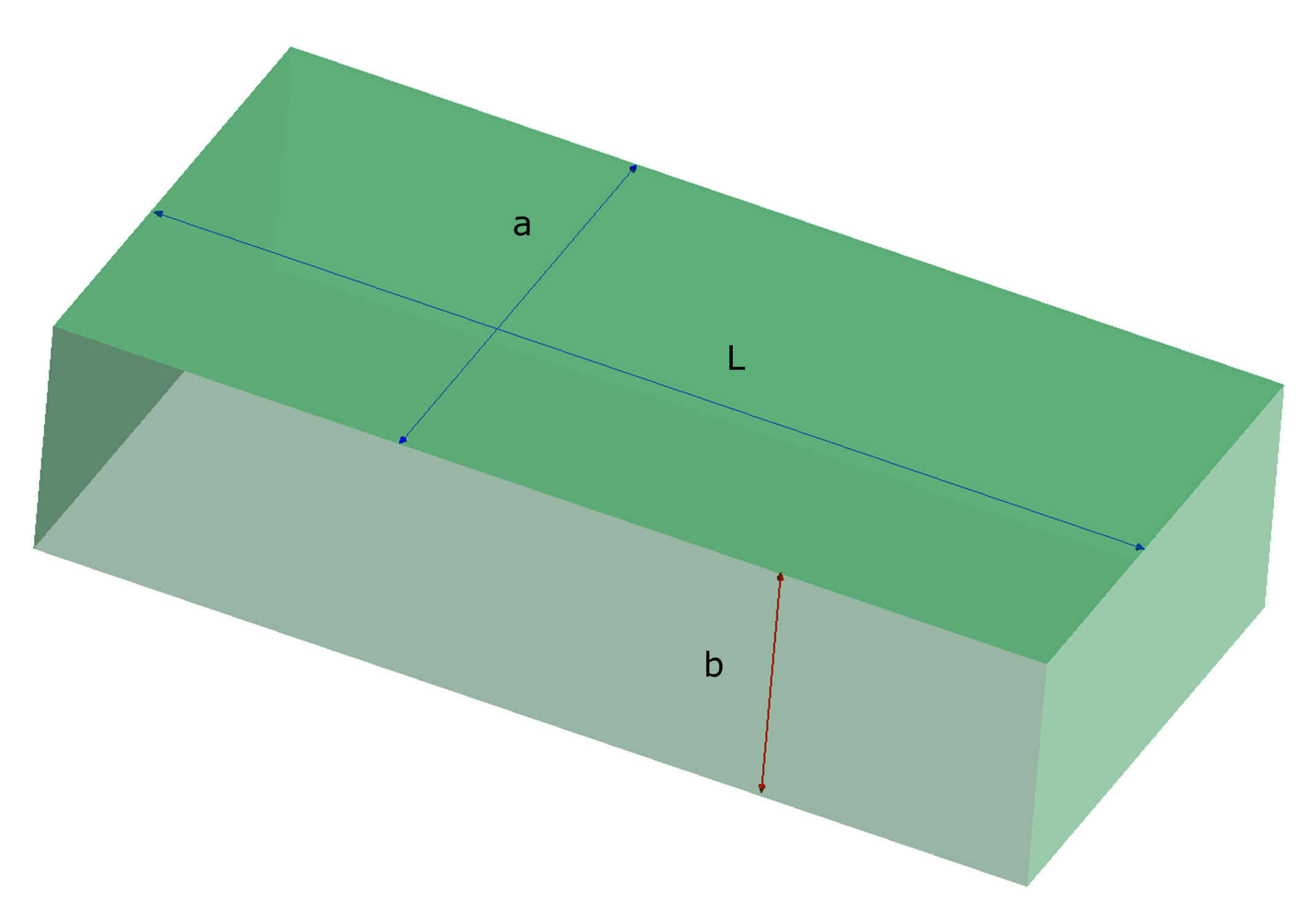
- 図 1:a = 20mm、b = 10 mm、L = 40 mm
- すべての壁面はPEC(完全電気導体)条件下となります
- 特性
- 値
- 誘電体の比誘電率( )
- 1.0
- 誘電体の比透磁率( )
- 1.0
- 電導率( )
- 1.0 [S/m]
基準解
このケースの電界強度の方程式は1です。
この問題の条件下における調和波(時間依存性 を持つ)は、次の形式を取ります。
- 透磁率
- 誘電率
- 材料の固有インピーダンス
- 材料の光速
固有周波数を求めることは、二次方程式の解に帰着します。
- 減衰定数
- 位相定数(波数)
の場合、位相定数はゼロとなり、振動は観測されません。そのようなモードが励起された場合、ゼロに減衰しているはずです。 の場合、モードは振動し、周波数 に依存しない時間定数 によって定義される速度で減衰します。
結果
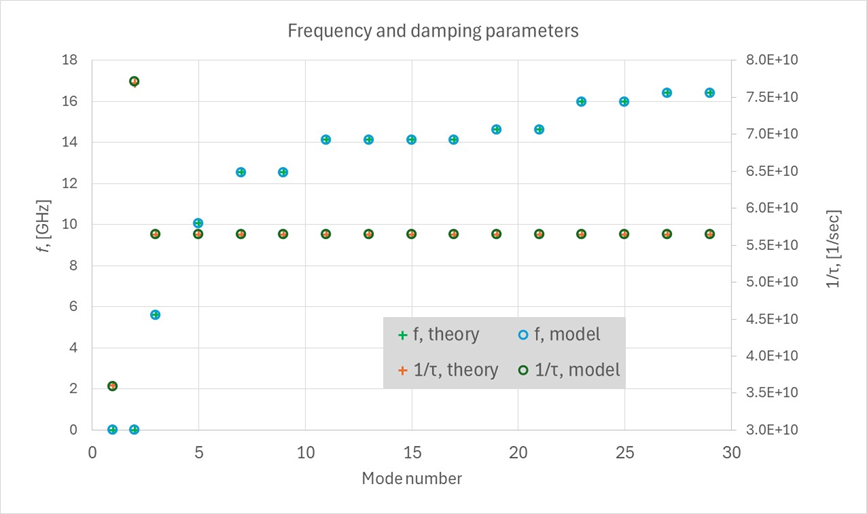
モードについて、理論値fと、モデリングで得られた値
の比較を、以下の図に示します。Figure 2. 理論値とモデル共振パラメータの比較(複素共役値は示していない)

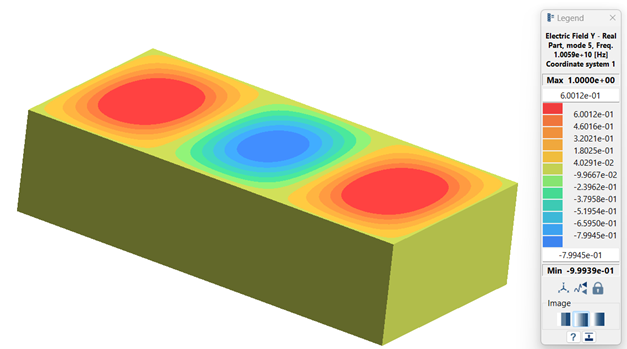
以下の図は、あるモードの電界分布を示しています。Figure 3.
モードの電界
の分布の実数部

1 Jianming, J., The finite element method in electromagnetics, 3rd Edition, John Wiley & Sons, Inc., 2014, Ex.12.8.
2 Pozar, D.M., Microwave Engineering, 4th Edition, John Wiley & Sons, Inc., 2012, §6.3.